具体的な目標点数・押さえておきたい単元

それでは具体的な対策例を見てみましょう。

【注目の設問①　 H25　2】

A地点からB地点まで向かって一定の速さで流れている川があります。この川のA地点からボールを流し、同時にB地点からA地点に向けて船が出発しました。船がA地点で折り返して、B地点まで一往復したところ、船がB地点に到着してから42秒後にボールもB地点に到着しました。 　船がB地点からA地点まで行くのにかかった時間は、船がA地点からB地点まで行くのにかかった時間の2.25倍でした。船の静水での速さは一定として以下の問いに答えなさい。

(1) ボールがA地点を出発してからB地点に到着するまでに何分何秒かかりましたか。

(2) 船とボールが出発してから、(ア)最初に出会うまでのかかった時間、(イ)船がボールに追いつくまでにかかった時間、をそれぞれ求めなさい。〔～分～秒〕

【解答解説】

(1) まず「距離AB間が一定」ということより、 「かかる時間の比←逆比→速さの比」の関係を用いて、問題文中で示された「量の関係」を整理します。
　　　　　　　　　　　　　　　　　　　　　　 B→A(上り)：A→B(下り)〔時間〕＝2.25：1＝9：4 　　　　　　　　　　　　　　　 　　
　　　　　　　　　　　⇓ 　　　　　　　　　　　　　
B→A(上り)：A→B(下り)〔速さ〕＝4：9
　　　　　　　　 　　 ⇓
上り：下り：流れ〔速さ〕＝4：9：(9－4)÷2＝8：18：5
　　　　　　　　　　　⇓
上り：下り：流れ〔時間〕＝1÷8：1÷18：1÷5＝45：20：72

次に、これらの関係を利用して「グラフ1」にまとめます。
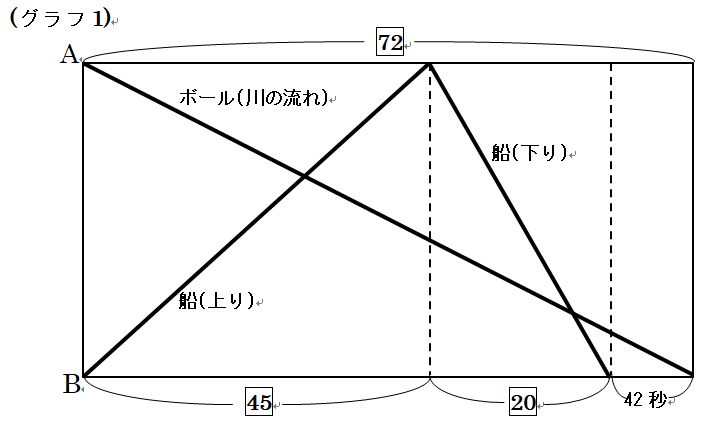　グラフ1より、比の(72－45－20＝)7が42秒にあたりますから、求める「ボールが A地点を出発してからB地点に到着するまでの時間(72)」は、42÷7×72＝432秒より、 7分12秒です。

(2)　 (1)で示したグラフ1を利用し、図形的に解いてみます。
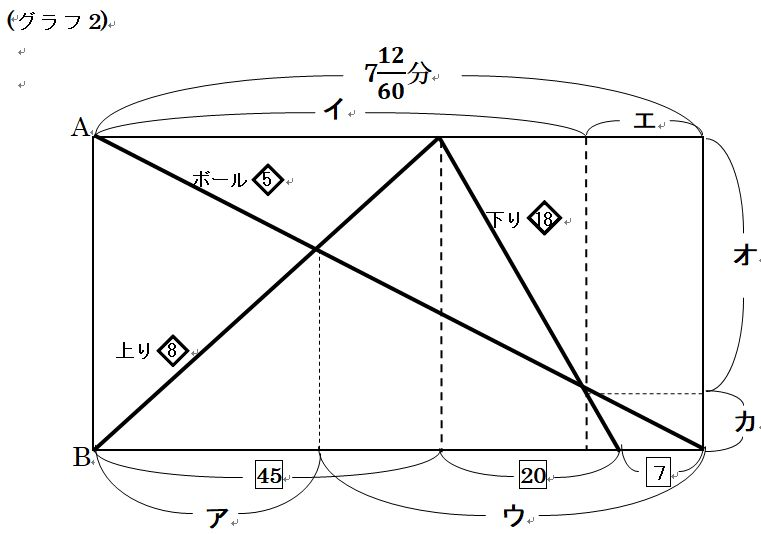グラフ2で、最初に出会うまでの時間はア、船がボールに追いつくまでの時間はイとなります。アとウの比は、上りとボールの速さの比の逆比で5：8ですから、
アは712/60÷(5＋8)×5＝210/13分より、2分462/13秒です。　(60×10/13＝462/13)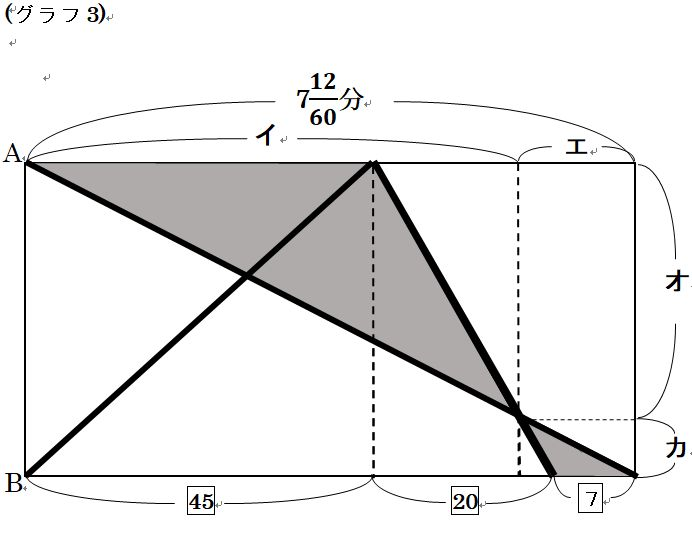
グラフ3で示した相似に着目すると、オとカの比が45：7となりますから、イとエの比(直角三角形の相似に着目)も45：7となります。
よってイは712/60÷(45＋7)×45＝63/13分より、6分1311/13秒です。(60×3/13＝1311/13)

以上のように開成の算数入試問題は、途中の考え方をみる「大学受験の数学と同じ形式」ですから、式と論理で押し通すだけでなく「ビジュアルにうったえる」ことも有効な解法となります。よって図・表・グラフの利用を心がけてください。

特に図形の問題は、解答用紙にも必ず同じ図形を設けていますので、それを活用しない手はありません。

【注目の設問② H23 4】

図のような、1辺が12cmの 立方体があります。辺AD上に点 Pと点Sが、辺AB上に点Qが、 辺BF上に点Rが、辺FG上に点 Tがあり、AP＝3cm、AS＝AQ＝ BR＝FT＝6cmです。 この立方体を3点P、Q、Rを通る平面、 および3点S、B、Tを通る平面で切ります。 図には切るときの様子の一部分を、正確では ありませんがかいてあります。 このとき、次の問いに答えなさい。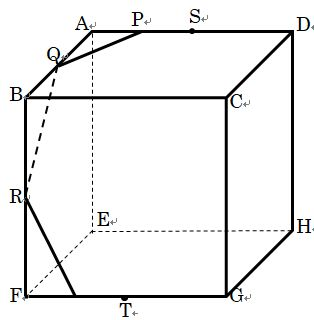
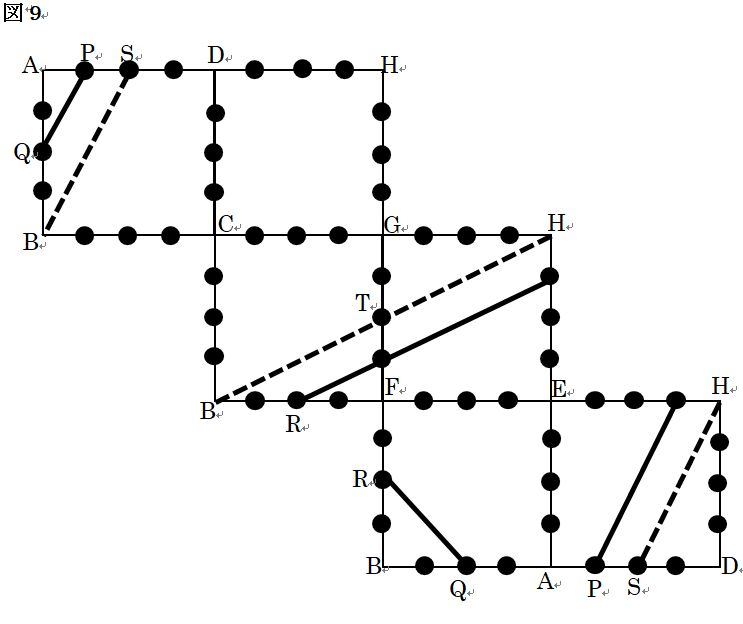
(1) この立方体を3点P、Q、Rを通る平面によって切ったとき、立方体の表面にできる切り口を、展開図に実線(　　)ですべてかき入れなさい。さらに3点S、B、Tを通る平面によって切ったとき、立方体の表面にできる切り口を、展開図に点線で(・・・)すべてかき入れなさい。

(2) 2つの平面で切ったときにできた3つの立体のうち、頂点Aを含む立体Xおよび頂点Aも頂点Cも含まない立体Yの体積をそれぞれ求めなさい。(単位：$cm^3$)
ただし、三角すいの体積は、「底面の三角形の面積×高さ÷3」で求めることができます。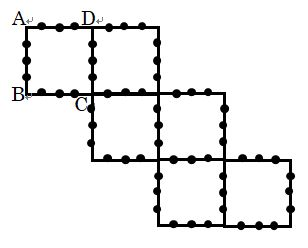
【解答解説】

(1) 今ではさほど珍しくはない「立体切断の典型問題」です。「三角すいをつくって捉える」の 　が基本対策です。
まず3点P、Q、Rを通る面を寸法が示されている面から順に捉えていきます。 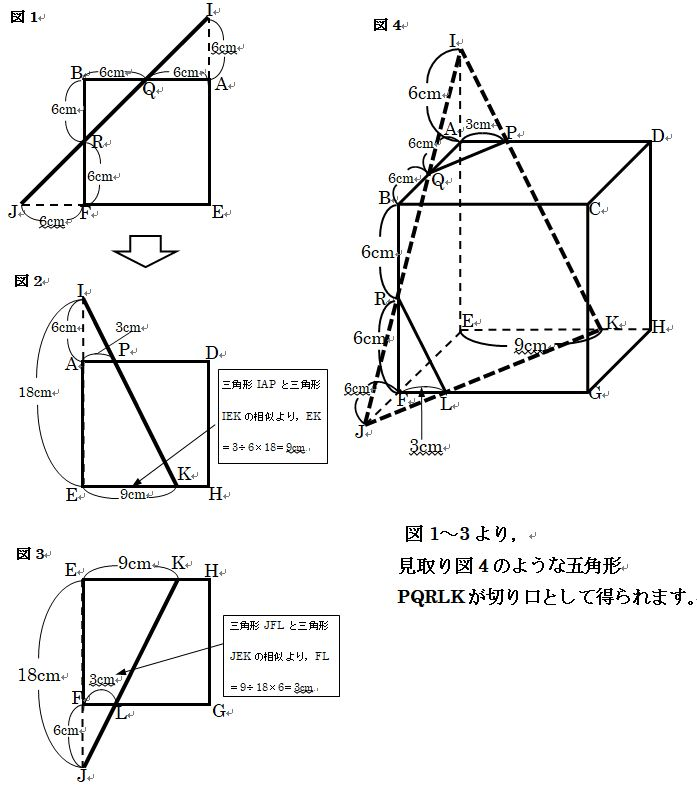同様に3点S、B、Tを通る面を寸法が示されている面から順に捉えていきます。 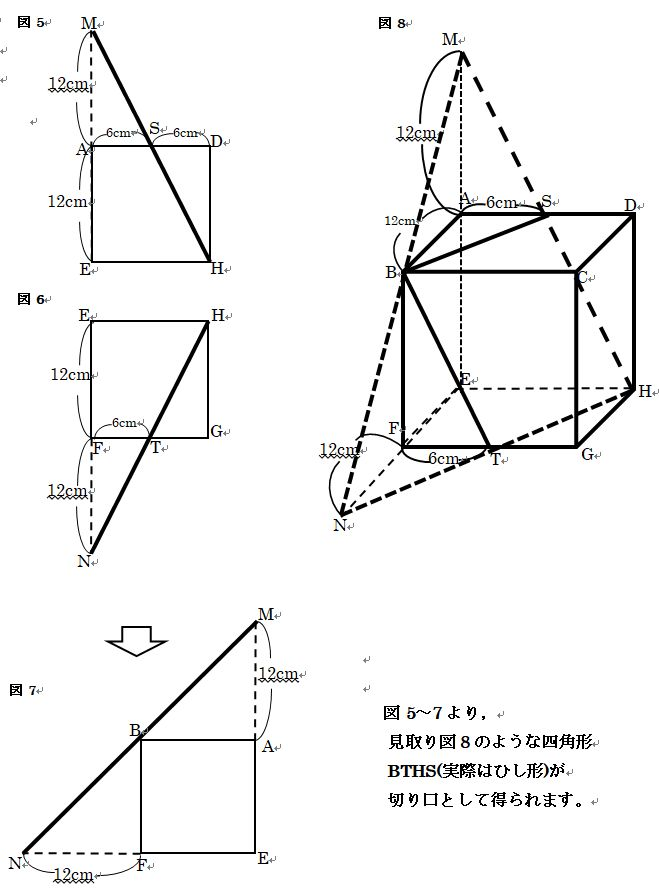あとは、立体の展開図の頂点に見取り図の頂点を(辺上の点も)かきこみ、3点P、Q、Rを通る切り口PQRLK、3点S、B、Tを通る切り口BTHS、をそれぞれ実線、点線で展開図にかきこんだものが図9です(LとKは図中では省略)。
(2) 　(1)で求めた見取り図を利用すると 　立体Xの体積は、三角すいI-EJKの 　体積から、三角すいI-AQPの体積と 　三角すいJ-RFLの体積をひいたもの 　です(図10)。よって、 　 　

18×9÷2×18÷3 －(6×3÷2×6÷3＋6×3÷2×6÷3) ＝450cm3となります. 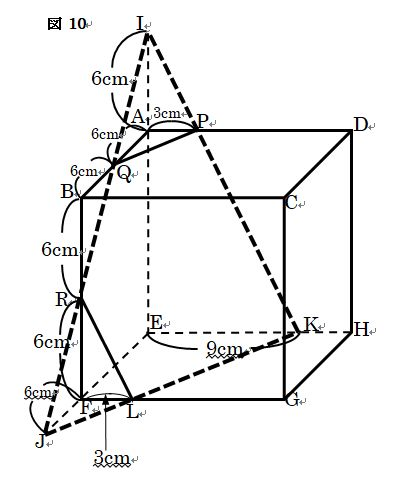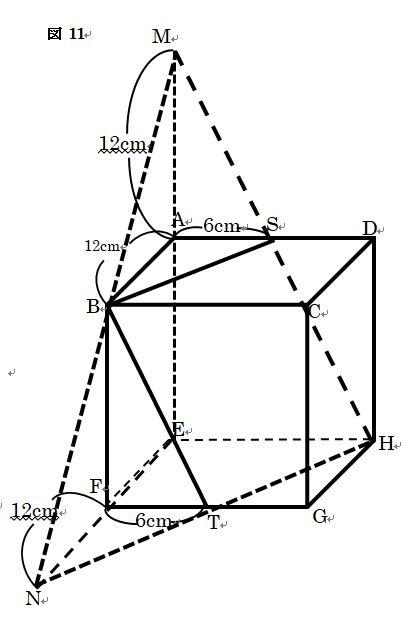見取り図11より、 3点S、B、Tで切断したときのAを 含む方の立体が、立体Xと立体Yを 合わせたものです。この体積は、 三角すいM-ENHの体積から、 三角すいM-ABSの体積と 三角すいN-BFTの体積をひいたもの ですから、

$24 \times 12 \div 2 \times 24 \div 3 -\left( 12 \times 6 \div 2 \times 12 \div 3+ 12 \times 6 \div 2 \times 12 \div 3 \right) =864 cm^3$となります。

よって立体Yの体積は、 864－450＝414 cm3となります。

※この問題の場合、立方体を面BTHSで2つ に切ると、合同な2つの立体に分かれるので、 立体Xと立体Yを合わせた立体の体積は、 12×12×12÷2＝864cm3として求めることも できます。

立体切断は、開成では「典型問題」と位置付けられるもので、最近は頻度が低くなっているとはいえ、いつ出題されてもおかしくない重要単元といえます。よって「大問４」で出題されても、このレベルであれば「完全解答」を目指す必要があります。

今回は「投影図」を利用して各面の相似の様子を詳しく示していきましたが、慣れてくれば、立体の見取り図に情報の処理を直接かきこんでいけるようになるはずであり、そこまでの準備が必要です。　
最近の中学受験算数の傾向として、御三家に次ぐレベルの中学(海城等)では、御三家よりも難度の高い立体切断を出題していますので注意が必要です。

【注目の設問③ H30 1　(1)】
　
次の□には同じ数が入ります。あてはまる数を求めなさい。

$0.1875 \times \left( 1\frac{1}{3} －\triangle \right) ＝\left( \frac{17}{21}－\triangle \right) \div 1\frac{1}{7}$

【解答解説】

$0.1875 \times \left( 1\frac{1}{3} －\triangle \right) ＝\left( \frac{17}{21}－\triangle \right) \div 1\frac{1}{7}$
↓＜帯分数⇒仮分数、小数⇒分数、割り算⇒掛け算＞
$\frac{3}{16} \times \left( \frac{4}{3} - \triangle \right) = \left ( \frac{17}{21} - \triangle \right) \times \frac{7}{8}$
　　 ↓＜逆比処理＞
(4/3－□)：(17/21－□)＝16/3：8/7＝14：3 ↓＜線分図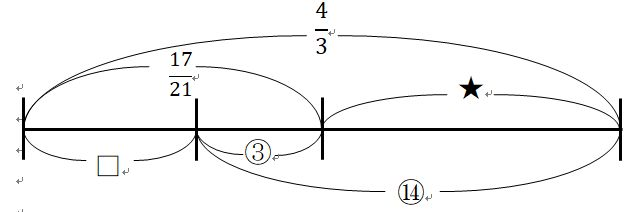＞ 　上の★の部分で、⑭－③＝⑪が、4/3－17/21＝11/21にあたりますから、
①は11/21÷11＝1/21です。
よって、求める□は、4/3－1/21×14 (＝17/21－1/21×3)＝2/3となります。

一見普通の「逆算」と思いきや、「未知数□が2個ある」ということで「一般的に小学生では解けない、文字計算を必要とする方程式」であることがわかり、「開成の受験には方程式の習得が必要」という解釈もできます。

しかし、方程式を利用したとしても、「数値が面倒かつ1問目」ということで計算間違いが起きやすく、仮にここを正解できたとしてもペースを乱されてしまい結果的に合格点に届かなくなる可能性が高くなってしまいます。

同時にこれらの問題は「中学受験の算数」として出題されていますので、実はこの問題は「方程式を使わずに解けるか否かを試している」という解釈もでき、ここで「工夫」することが以降の問題を自分のペースで解き進めることにも繋がり、より合格に近づくことにもなるのす。

【まとめ】

以上、高難度ではありますが冒頭で触れた「特に強化すべき単元」から代表的な開成中学の算数入試問題をご紹介いたしました。

開成中学の入試問題に対応するためには「図形・速さ・数論」だけ強化しておけばよいのではなく「どんな単元が出題されても落ち着いて対応できる力」すなわち「真の実力」をつけておく必要があります。栄養バランス・運動能力バランスなどと同様に「偏りのない学習」によってバランス良く高い学力が身に着くよう心がけていただき、小学6年生のなるべく早い時期に「過去問等を利用した実戦演習」を開始することが重要です。 御三家をはじめとする中学受験の算数に特徴的な「記述力(途中の考え方を示す力)」を磨き、国語・社会・理科と同様に「答案

用紙」を添削してもらう習慣をつけること、さらには「問題用紙をどう活用しているか?」を客観的に考察することも合格への重要なカギとなるはずです。

家庭教師アルファ・ネクサスでは、中学受験の算数の基礎から記述力、思考力を試される高度な問題まで、職人のような一流プロ家庭教師が具体的な解決策を提示。がんばる中学受験生を志望中学合格に導きます。

Contact Us

▲「ネッ犬（ねっけん）」くん

会社連絡先

住所
■ 本社オフィス
▶東京都中央区日本橋本石町2‐1‐1
アスパ日本橋オフィス

■ 中野オフィス
東京都中野区中野1-30-23-101

電話:
03-5389-3995

E-mail:
info@alpha-nexus.jp

受付時間:
10:00-22:00