
問1 54で割ると6余る、3けたで最も大きい整数は( )です。
問2 54を割ると6余る、最も小さい整数は( )です。
★解答・解説
「~で割る」 「~を割る」は、特に中学受験を目指す低学年の生徒さんを混乱させることが多いようです。
例えば、25÷6=4 あまり 1
これを言葉で表すと、
25 を 6 で わると 商が4で余りが1
となります。
もしも迷った場合は、このように例えをつくってみますと、約数と倍数のどちらが関連するかが判断できると思います。
問1
求める数を□とし、商を△とすると、□÷54=△あまり6、
となりますので、□=△×54+6となり、
□は、54の倍数に6を加えた整数ということになります。
この条件のうち、3けたで一番大きい整数ですから、
999÷54=18あまり27より、求める整数は、
999-27+6(=54×18+6)=978より
978
となります。
問2
求める数を□とし、商を△とすると、54÷□=△あまり6、となりますので、
54=□×△+6となり、
□は、(54-6=)48の約数で6より大きい整数(割る数□は余りより大きい)ということになります。
48の約数は、1,2,3,4,6,8,12,16,24,48
ですが、余りの6よりも大きくなければならないので、6以下の整数は当てはまりません。
よって求める整数は、残った48の約数のうちで最も小さい整数となり、8です。
問1 赤青黄緑のカードを、それぞれ1枚ずつ1列に並べる方法は全部で( )通りです。
問2 赤のカード2枚、青のカード3枚、全部で5枚のカードを1列に並べる方法は全部で( )通りです。ただし、同じ色のカードに区別はありません。
★解答・解説
場合の数は、大きく分けて「並べ方(順列)」と「選び方(組み合わせ)」の2つに分かれます。
問1は、問題文にも「並べる方法・・・」とあるので、順列の処理で解きます。
問1
樹形図で考えます。
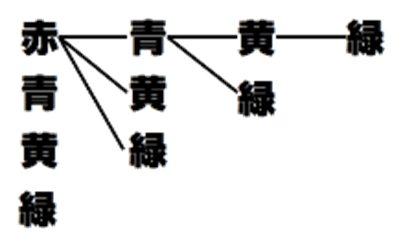
上の樹形図より、4×3×2(×1)=24より24通りです。
問2も、問題文にも「並べる方法・・・」とあるので、順列で処理しておきます。
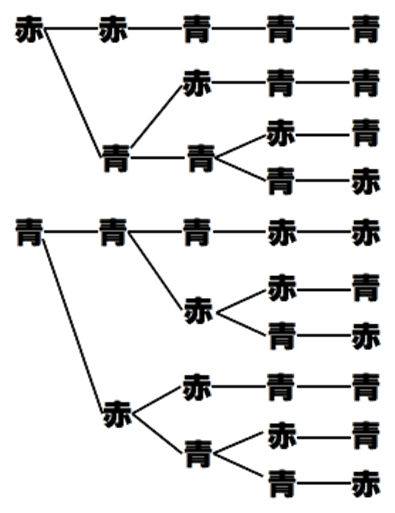
上の樹形図のように、左端に赤がくる場合が4通り、左端に青がくる場合が6通りで、4+6=10より10通りとなります。
ところが、ご覧のように、「赤2枚」「青3枚」を意識しながら樹形図をかかなければならず、このやり方では枚数が増えた場合、大変間違いやすいです。一見この問題は「順列で解く」流れに見えますが、実は同じ色のカードの区別がないため、カードを置く5か所のうち、赤のカード2枚を置く場所を決めることにより、残り3か所が自動的に3枚の青のカードとなるため、 赤のカード2枚を置く場所を、5か所から選ぶ組み合わせということになり、「組み合わせで解く」ことができます。
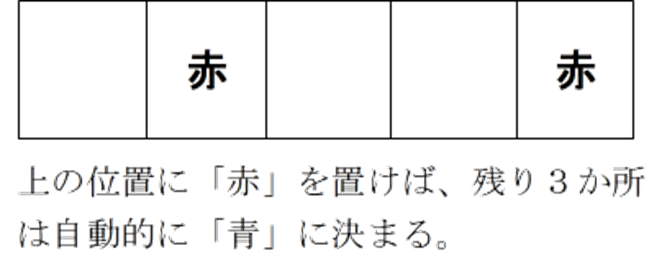
1枚目の赤のカードを置く場所が5か所、2枚目の赤のカードを置く場所が、残りの4か所となり、5×4=20より20通りですが、1枚目と2枚目のカードを置く順番は考えないため、
20÷2=10より、この解き方でも10通りとなります。
中学受験の算数では、一般的にこのパターンの問題は「組み合わせ」として処理されます。
住所: 東京都中野区中野1-30-23-1F
電話: 0120-02-5335 03-5389-3995
E-mail: info@alpha-nexus.jp
受付時間: 9:00-24:00